.
《 質疑応答 》
.
《Q-1》 論理学が このように変革されたとなると、今迄の数学上の諸成果.は みんな 宙.に浮いてしまう/疑わしいものになってしまうのか?
---> Ans.
《Q-2》 従来、帰謬法とは.「命題.Aを.証明するのに Aの否定から矛盾を導く論法.」.であるとされて来たし、自分もそのように理解してきたの.
だが、講演者が.帰謬法の原理としてあげている論理法則.を.見ると 従来の見解とは異なるようなのだが 如何?
--->Ans.
Ans
.
《Q-3》.'ライオンは哺乳動物である'は'ライオンもクジラも共に哺乳動物である'を内含しない.との話だったが、'ライオンは哺乳動物である'.
は真であり.'ライオンもクジラも共に哺乳動物である'も真なのだから.'ライオンは哺乳動物である'は'ライオンもクジラも共に哺乳動物である'.
を内含すると言えるではないか?---> Ans.
.
《Q-4》 四階の真理.には どんなものがあるのか? ---> Ans.
.
《Q-5》 五階以上の真理.は どうして存在しないのか? ---> Ans.
.
《Q-6》 講演者は、[PはQを内含する]が偽であるのに[Pでないか又はQである]は真となるような.事例.を.あげて、[PはQを内含する]と.
.[Pでないか又はQである]とが同義ではないと主張しているが、[Pでないか又はQである]は[PはQを実質的.に内含する]であって、[Pは.
Qを内含する]よりは"広義である"とされていたのだから、[PはQを内含する]が真である場合に[Pでないか又はQである]が常に真であり.
さえすればよいのであって、[PはQを内含する]が偽である場合に[Pでないか又はQである]が真となることがあっても.別.に差し支えはない.
のではないか?.---> Ans
.
《Q-7》 仮言命題.や.内含.の新定義.を.聞.かせて貰ったけれど.も、あれだ.と.次.のような矛盾.が生ずる筈.なのだが、如何?.---> Ans.
.
《Q-8》 Fregean理論では [PならばQである] と [PはQを内含する] とを 同義と見做している との話だったが、自分が学んだ教科書では.
"PがQを内含する".とは."P⊃Qが恒真式である"ことを言う.と定義されていたと思うのだが ・・・。.---> Ans.
.
《Q-9》 [P(.x.) ならば Q(.x.) である]ことの意味が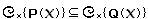 のことと定義されるとの話だったけれど、むしろ、A.⊆B.の
ほうが[x.∈A.ならば.x.∈B.である]のことと定義されるのではないのか?---> Ans.
のことと定義されるとの話だったけれど、むしろ、A.⊆B.の
ほうが[x.∈A.ならば.x.∈B.である]のことと定義されるのではないのか?---> Ans.
.
《Q-10》 真理.に階層があるという話.には納得できるが、実在.にも.それ応じた階層があるとするのは飛躍ではないか? .個別科学の法則.と.
論理法則.とで.は.言語上の位階.は確かに異なるけれども、.どちらも"言語で表わされたもの"という点では同.じであるから、存在の様式.は同.
じではないのか? ---> Ans.
.
《Q-11》 Venn図..は《.変項を一つだけ持つ述型.》.に対.してだけしか使えないのではないのか?---> Ans.
.
《Q-12》 仮言三段論法の原理の"二階のVenn図.による証明"なるものを見せてもらったけれど、論証を..あの様な幾何学的図形.に頼るの
は.妥当ではないのではないのか? ---> Ans.
.
《Q-13》 超論理法則 I,II で "充分である" とあるが、"必要充分である" とは言えぬのか?
もしそれが言えたら、"新論理学"は 旧来のものに帰着してしまうように思えるのだが ・・・ 。 ---> Ans.
.
《Q-14》 命題.Pが偽であるとは 〜Pが真であることに他ならないのだから、Pが偽であれば..そのことから.〜Pが導かれ、結局、〜P&.P.
が導かれることになるから、《矛盾ではなくて、単.に偽であるような命題.》.からでも.任意の命題.が導かれる.ので.は? ---> Ans.
.
《Q-15》 "旧理論"では.優勢を誇っていた.Hilbert.流の形式主義.が."新理論"では.全く影を潜めてしまっているのは.何故.か? ---> Ans
.
《Q-16》 "新論理学"での.「仮言命題.」の定義.には."集合の包含関係".が使われているが、"新論理学".は.集合論.に基礎.を.置.いている.
と考えてよいのか? ---> Ans.
.
《Q-17》 仮言命題を "カテゴリー空間"の間.の包含関係.によって定義するとのことだったが、"カテゴリー空間"のかわりに"真理集合"ではだめなのか? ---> Ans.
.
《Q-18》 講演者が."フレーゲアン理論".と呼んでいる理論.は、普通.は."古典論理".と呼.ばれている筈なの.に、どうしてそう呼.ばず.に、わざ
わざ."フレーゲアン理論".などと.呼ぶのか?
---> Ans.
.
《Q-19》 "命題論理"と これまで呼ばれていたものには、新論理学ではどんな位置づけがなされるのか? ---> Ans.
.
《Q-20》 "新論理学"で表わされることは 従来の"述語論理"でも 表わされはしないのか? それに、別.に"述語論理"に 矛盾があるわけではないのだから、数学.に関する限り.は これ ―― 述語論理 ―― で充分.間.に合うのではないのか? ---> Ans .
.

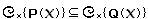 のことと定義されるとの話だったけれど、むしろ、A.⊆B.の
ほうが[x.∈A.ならば.x.∈B.である]のことと定義されるのではないのか?---> Ans.
のことと定義されるとの話だったけれど、むしろ、A.⊆B.の
ほうが[x.∈A.ならば.x.∈B.である]のことと定義されるのではないのか?---> Ans.
